
L'acide Isocyanique (HNCO)
Modélisation de la molécule de HNCO: Calcul des fréquences de vibration et représentation des modes
(Extrait du Chapitre 1 de la Partie 1 de ma thèse)
Les différents paramètres optimisés de la géométrie de HNCO, sont obtenus par calculs quantiques (MP2/6-31G(d,p) et B3LYP/6-31G(d,p)) et sont comparés aux données expérimentales obtenues par spectroscopie rotationnelle et recueillies par Yamada [1]. Ces paramètres sont notés sur la figure 1 et reportés dans le tableau 1.

Figure 1. Géométrie optimisée de HNCO et charges des atomes obtenues en B3LYP et MP2 (italiques)
|
|
Valeurs Théoriques |
Valeurs Expérimentales |
|
|
|
MP2 |
B3LYP |
|
|
r1 |
1,005 |
1,008 |
0,995 |
|
r2 |
1,226 |
1,219 |
1,214 |
|
r3 |
1,185 |
1,174 |
1,166 |
| q1 |
124,4 |
124,7 |
123,9 |
| q2 |
171,8 |
172,2 |
172,6 |
Tableau 1. Valeurs théoriques obtenues par MP2 et B3LYP et expérimentales des liaisons (Å) et angles (degrés) de HNCO
Un excellent accord est observé entre la géométrie calculée par ses deux méthodes et la géométrie expérimentale. Cette géométrie nous servira donc de point de départ pour tous nos calculs quantiques impliquant HNCO.
HNCO est un rotateur asymétrique appartenant au groupe de symétrie Cs. Cette molécule possède 6 modes de vibration, tous actifs en infrarouge :
- 5 de symétrie A' (noté de n1 à n5)
- 1 de symétrie A'' (noté n6)
Le calcul du spectre vibrationnel est effectué au même niveau théorique que celui de la géométrie. Les fréquences obtenues sont présentées dans le tableau 2.
|
|
Fréquences théoriques (cm-1) |
Intensité (%) |
Symétrie |
Attributions |
|
|
|
MP2 |
B3LYP |
|||
| n1 |
3791,1 |
3701,2 |
23,1 |
A' |
nNH |
| n2 |
2366,3 |
2356,6 |
100,0 |
A' |
nNCO asym. |
| n3 |
1310,1 |
1338,7 |
0,1 |
A' |
nNCO sym. |
| n4 |
793,9 |
792,0 |
37,3 |
A' |
dHNC |
| n6 |
610,3 |
610,5 |
0,5 |
A'' |
dNCO |
| n5 |
559,1 |
559,4 |
12,0 |
A' |
dNCO |
Tableau 2. Fréquences théoriques, intensités, symétries et attributions des différents modes de vibration de HNCO (n pour élongations, d pour déformations)
Les six modes de vibration sont représentés sur la figure 2.
- Le mode n1, correspond à l'élongation (vibration A') de la liaison NH.
- Le mode n2, correspond à l'élongation (vibration antisymétrique A') du groupement NCO.
- Le mode n3, correspond à l'élongation (vibration symétrique A') du groupement NCO.
- Le mode n4, correspond à la déformation angulaire (A') entre les liaisons HNC.
- Le mode n5, correspond à la déformation angulaire (A') entre les liaisons NCO.
- Le mode n6, correspond à la vibration hors du plan (A") du groupement NCO.
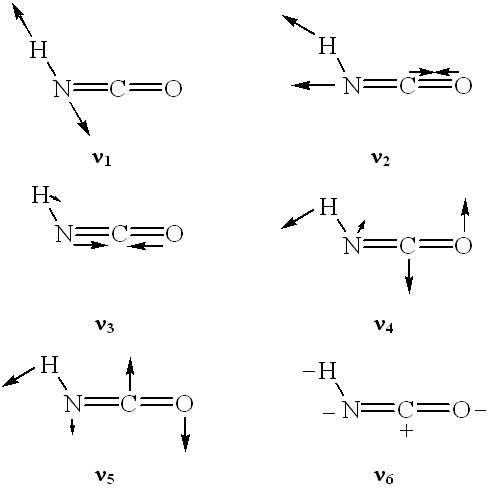
Figure 2. Représentations des différents modes de vibration de HNCO isolé
(Les modes sont animés si on clique dessus)
Nous pouvons comparer les fréquences expérimentales retenues pour la molécule en phase gazeuse et isolée en matrice cryogénique d'argon et les comparer avec nos fréquences théoriques (B3LYP) pondérées.
|
Modes |
Fréquences (cm-1) |
Attributions |
|||
|
Expérimentales |
Théoriques (B3LYP/6-31G(d,p)) |
||||
|
Phase gazeuse |
Matrice |
Non pondérées |
Pondérées * |
||
|
n1 |
3531 |
3511,5 |
3701,2 |
3516,1 |
nNH |
|
n2 |
2274 |
2259,0 |
2356,6 |
2238,8 |
nNCO asym. |
|
n3 |
1327 |
- |
1338,7 |
1271,8 |
nNCO sym. |
|
n4 + n5 |
1371 |
1315,0 |
1351,4 |
1324,4 |
|
|
n4 |
|
770,0 |
792,0 |
776,2 |
dHNC |
|
n6 |
|
697,0 |
610,5 |
598,3 |
dNCO |
|
n5 |
|
573,5 |
559,4 |
548,2 |
dNCO |
Tableau 3. Fréquences expérimentales de HNCO en phase gazeuse et isolé en matrice d'argon (1/700), calculées en B3LYP/6-31G(d,p) pondérées et non pondérées.
* Les facteurs de pondération sont de 0,95 pour n1, n2, et n3, et de 0,98 pour n4, n5, et n6.
Ces résultats coïncident avec ceux obtenus par Teles et al. [2]
[2] J.H. Teles, G. Maier, B.A. Hess, L.J. Schaad, M. Winnewisser, B.P. Winnewisser, Chem. Ber., 122, 1989, 753.